QÜESTIONARI DE SELECTIVITAT JUNY 2015 SÈRIE 4
Instruccions sobre el funcionament del qüestionari
- Quan es comproven les respostes, en l'exercici 1 es motra si la resposta és correcta o incorrecta (sent verda si és correcta i vermella si no ho és).
- En tots els altres exercicis, la resposta incorrecta va seguida d'una finestra on es mostra la correcta i, en la majoria de casos, els passos a seguir per arribar a ella.
PRIMERA PART
Exercici 1
[2,5 punts en total][En cada qüestió només es pot triar UNA resposta. Qüestió ben contestada: 0,5 punts; qüestió mal contestada: –0,16 punts; qüestió no contestada: 0 punts.]
Qüestió 1
El palet estàndard europeu té unes dimensions de (800 × 1 200) mm2 i pot tenir una massa màxima, juntament amb la càrrega, de 1 000 kg. La base d’una prestatgeria que permet suportar aquest tipus de palets, de qualsevol massa autoritzada i sense apilar-los, és de (2 700 × 1 350) mm2 . Quina massa ha de poder suportar un prestatge d’aquesta prestatgeria?
Qüestió 2
Un motor de cotxe té quatre cilindres amb un diàmetre de 79,5 mm i una cursa de 80,5 mm cadascun. Quina és la cilindrada del motor?
Qüestió 3
Un tacòmetre digital mostra el valor de la mesura amb cinc dígits i permet fer mesuraments entre 1 min–1 i 99 999 min–1. La precisió és el valor més gran entre ± 0,02 % de la mesura o ± 1 min–1. Si el tacòmetre mostra 24 959 min–1, el valor real de la mesura està comprès entre:
Qüestió 4
Un cargol avança a una velocitat de 5 mm/s quan es cargola a 200 min–1. Quin és el pas del cargol?
Qüestió 5
En l’ajust 147 D9/h9, la tolerància D9 del forat és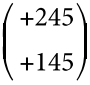 
μm i la h9 de l’eix és 
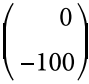μm.
Quin és el joc mínim d’aquest ajust?
Exercici 2
[2,5 punts en total]Es tiren simultàniament tres daus i se sumen els valors obtinguts. El resultat pot ser parell o senar en funció de si el valor de cadascun dels daus és, també, parell o senar. Es defineix la funció lògica de la paritat del resultat utilitzant les variables d’estat següents:
| \begin{align} dau &1:d_1=\begin{cases}1: senar \\ 0: parell\end{cases}; \end{align} | \begin{align} dau &2:d_2=\begin{cases}1: senar \\ 0: parell\end{cases}; \end{align} | |
| \begin{align} dau &3:d_3=\begin{cases}1: senar \\ 0: parell \end{cases}; \end{align} | \begin{align} resultat:r=\begin{cases}1: senar \\ 0: parell \end{cases} \end{align} |
a) Escriviu la taula de veritat del sistema. [1 punt]
b) Determineu la funció lògica entre aquestes variables i, si escau, simplifiqueu-la. [1 punt]
c) Dibuixeu l’esquema de portes lògiques equivalent. [0,5 punts]
SEGONA PART
OPCIÓ A
Exercici 3
[2,5 punts en total]Un dels cotxes participants en el Raŀli Dakar té un dipòsit de combustible amb una capacitat V= 400 L. La massa del vehicle amb el dipòsit buit més la dels ocupants és de m = 2 050 kg. El combustible que utilitza el cotxe és gasoil de densitat ρ = 0,832 kg/L i poder calorífic pc = 41,7 MJ/L. El radi de les rodes és r = 400 mm.
a) Dibuixeu, d’una manera aproximada i indicant les escales, la massa total en funció del percentatge de càrrega de combustible disponible en el dipòsit. [1 punt]
Amb la primera marxa, la relació de transmissió entre la velocitat de rotació del motor nmot i la velocitat de rotació de les rodes nr és τ = nr/nmot = 0,285. El rendiment de la transmissió és ηtrans = 0,85 i el motor proporciona un parell màxim Γ = 750 N m. Determineu:
b) El parell total màxim Γr a l’eix de les rodes. [0,5 punts]
c) L’acceleració màxima del cotxe amb el dipòsit ple i amb el dipòsit al 5 % de la capacitat total. [1 punt]
Exercici 4
[2,5 punts en total]Per a abastir d’aigua potable una població, es construeix una estació de bombament. Aquesta estació ha de bombar un volum diari V= 2 540 m3 elevant-lo a una altura h = 129 m. Les pèrdues de tota la instaŀlació són equivalents a una elevació addicional Δh = 70,81 m. L’estació de bombament consta de sis bombes accionades mitjançant un motor elèctric. El rendiment de les bombes és η = 0,7 i, per a reduir el cost de la despesa elèctrica, es bomba únicament durant un temps t = 8 h al dia en què el cost de l’energia elèctrica és el més reduït, i correspon a c = 0,08241 €/(kWh). Determineu:
a) El treball W que ha de desenvolupar l’estació de bombament. [1 punt]
b) La potència elèctrica Pelèctr consumida per cada bomba i el cost total del consum elèctric en un dia. [1 punt]
c) La pressió mitjana p de funcionament de les bombes. [0,5 punts]
OPCIÓ B
Exercici 3
[2,5 punts en total]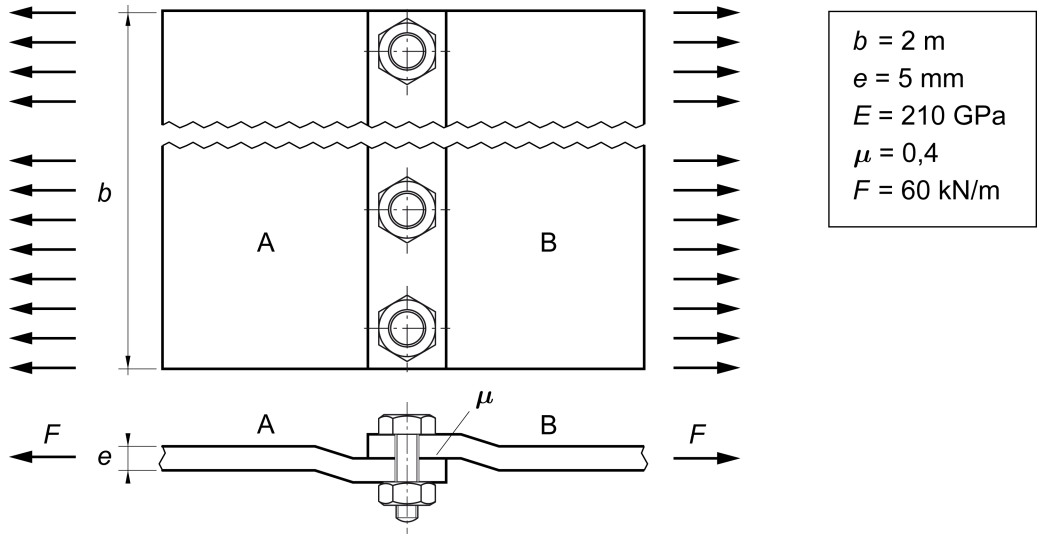
Les planxes d’acer A i B de la figura tenen un gruix e = 5 mm i una amplària b = 2 m. S’uneixen mitjançant cargols M10, que, collats d’una manera adequada, proporcionen una força de compressió de les planxes Fc = 32 kN. La unió de les planxes es produeix per la força de fricció que hi ha entre aquestes a causa de la compressió que hi exerceixen els cargols. El mòdul d’elasticitat de l’acer és E = 210 GPa i la unió ha d’aguantar una força distribuïda uniformement de F = 60 kN/m. Determineu:
a) El nombre de cargols que cal posar-hi. [1 punt]
b) La tensió normal σ de les planxes. [1 punt]
c) La deformació longitudinal unitària ε de les planxes causada per la força F. [0,5 punts]
Exercici 4
[2,5 punts en total]Un muntacàrregues és accionat per un motor reductor i un sistema de politges. El motor reductor és elèctric i té un rendiment ηmr = 0,65. El sistema de politges té un rendiment ηpol = 0,85 i proporciona una relació de transmissió entre la velocitat v de pujada de la càrrega, en m/s, i la rotació nmr de l’eix de sortida del motor reductor, en s–1, de τ = v/nmr = 0,9918 m. El motor s’alimenta amb una tensió U = 230 V i, en règim de funcionament nominal, consumeix una intensitat I = 6,4A quan la càrrega puja a v = 0,4 m/s constant. Determineu: