Results
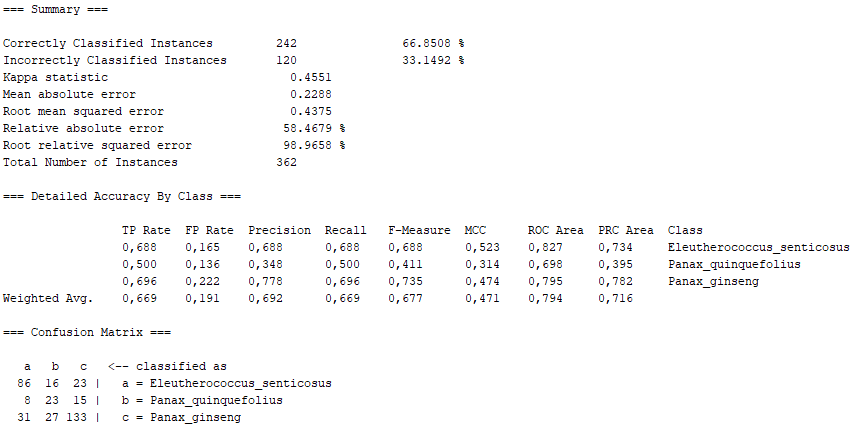
In this section, we expand on what was covered in the poster of the machine learning project (specifically, the WEKA part). In this case, we show the definition of the different algorithms used in the WEKA program, as well as the percentages obtained for "Correctly Classified Instances" and "Incorrectly Classified Instances", as well as the Confusion Matrix for each algorithm. In general, we show the Summary of the results obtained with the program WEKA, as well as a conclusion extracted from them.
K is an instance-based classifier, that is the class of a test instance is based upon the class of those training instances similar to it, as determined by some similarity function. It differs from other instance-based learners in that it uses an entropy-based distance function.

K-nearest neighbours classifier. Can select appropriate value of K based on cross-validation. Can also do distance weighting.
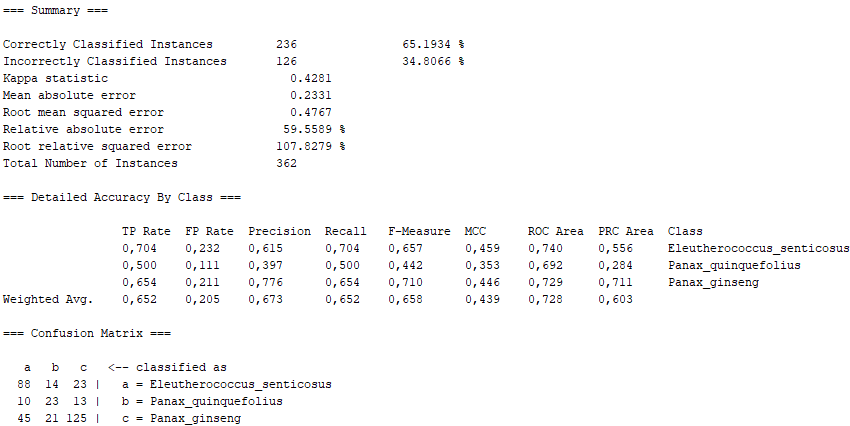
Sequential minimal optimization (SMO) is an algorithm for solving the quadratic programming (QP) problem that arises during the training of support-vector machines (SVM). It implements John Platt's sequential minimal optimization algorithm for training a support vector classifier. This implementation globally replaces all missing values and transforms nominal attributes into binary ones. It also normalizes all attributes by default.
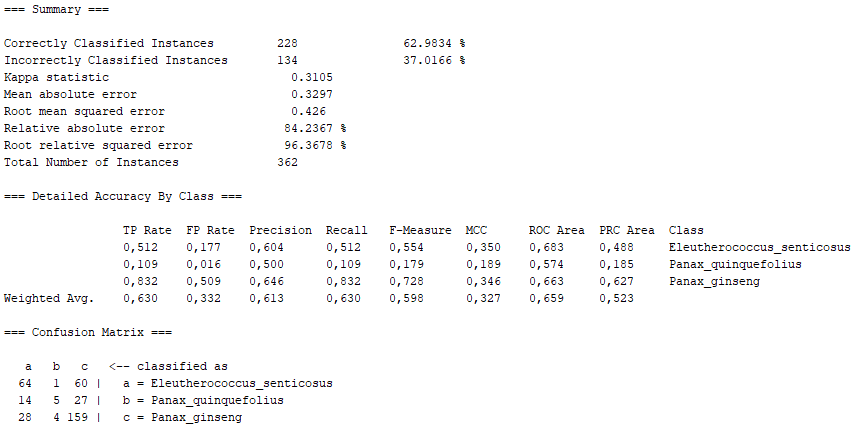
Class for building and using a multinomial logistic regression model with a ridge estimator. If there are k classes for n instances with m attributes, the parameter matrix B to be calculated will be an m*(k-1) matrix. In order to find the matrix B for which L is minimised, a Quasi-Newton Method is used to search for the optimized values of the m*(k-1) variables
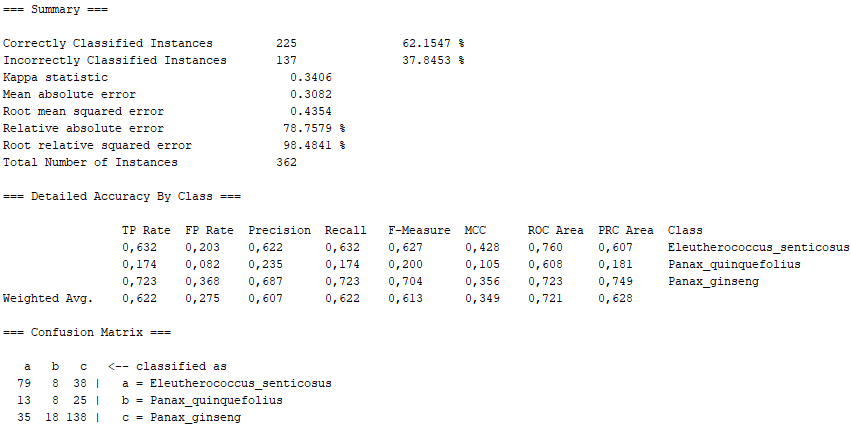
Classifier for building linear logistic regression models. LogitBoost with simple regression functions as base learners is used for fitting the logistic models. The optimal number of LogitBoost iterations to perform is cross-validated, which leads to automatic attribute selection.
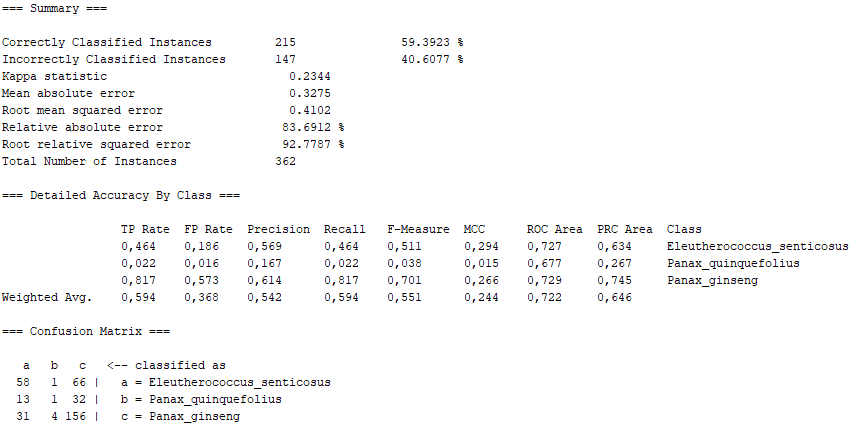
A wrapper for DeepLearning4j that can be used to train a multi-layer perceptron (classification and regression) using that library.
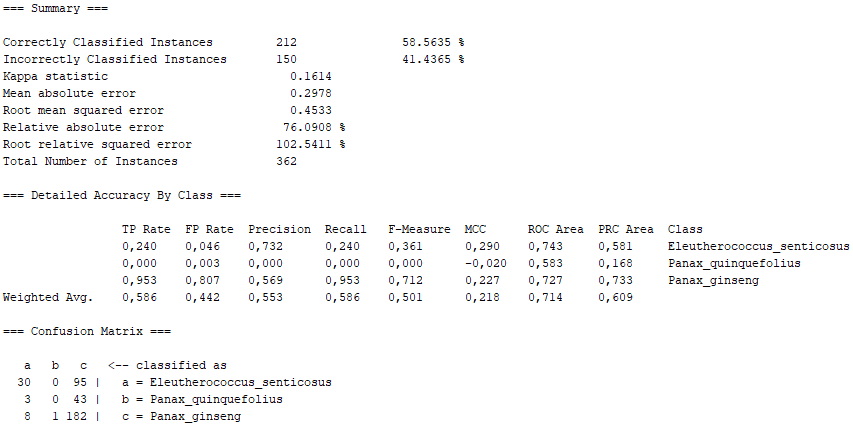
Class for constructing a forest of random trees. Random forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned. Random decision forests correct for decision trees' habit of overfitting to their training set. Random forests generally outperform decision trees, but their accuracy is lower than gradient boosted trees. However, data characteristics can affect their performance.
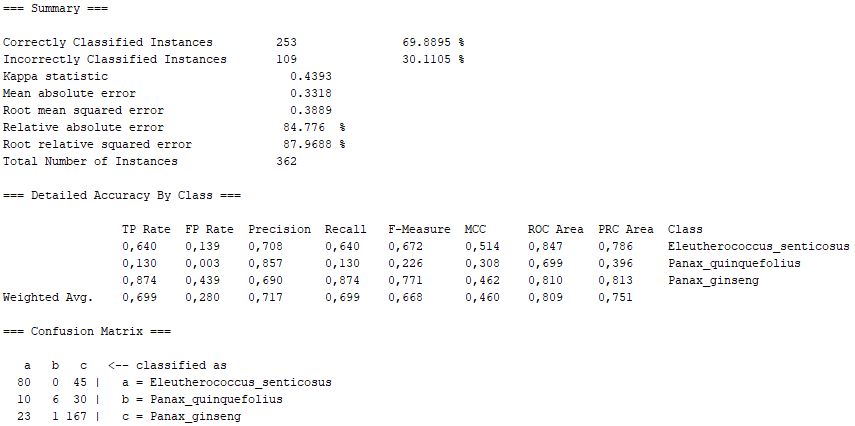
Class for generating a pruned or unpruned C4. It is a 5 decision tree.
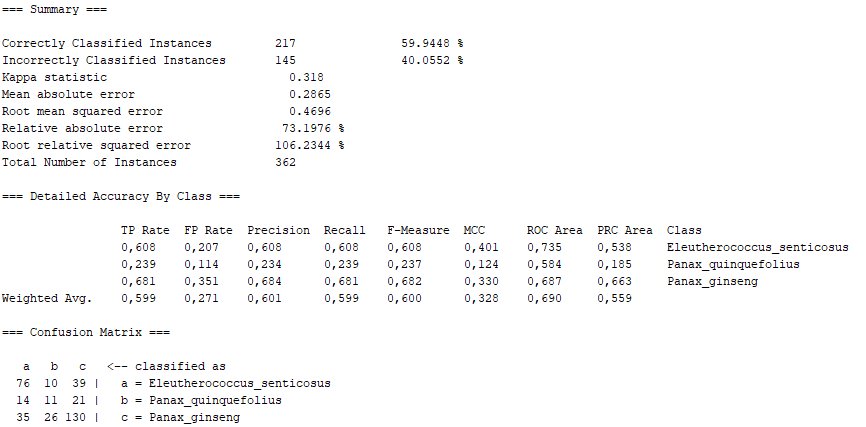
Class for constructing a tree that considers K randomly chosen attributes at each node. Performs no pruning. Also has an option to allow estimation of class probabilities (or target mean in the regression case) based on a hold-out set (backfitting).
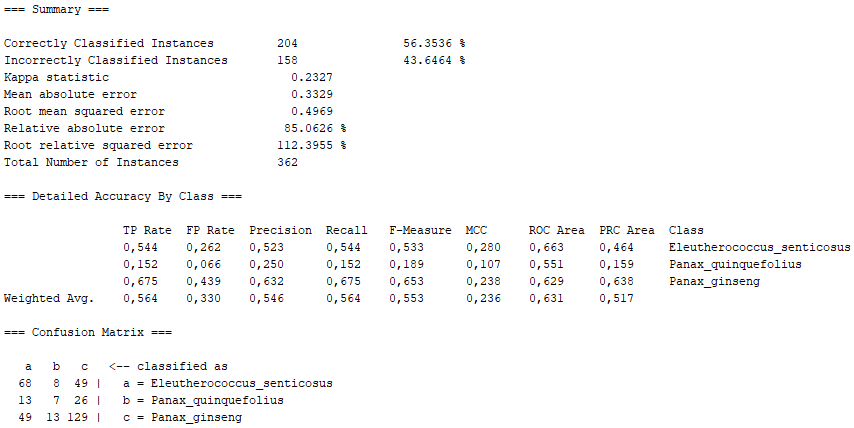
Bayes Network learning using various search algorithms and quality measures. Base class for a Bayes Network classifier. Provides datastructures (network structure, conditional probability distributions, etc.) and facilities common to Bayes Network learning algorithms like K2 and B.
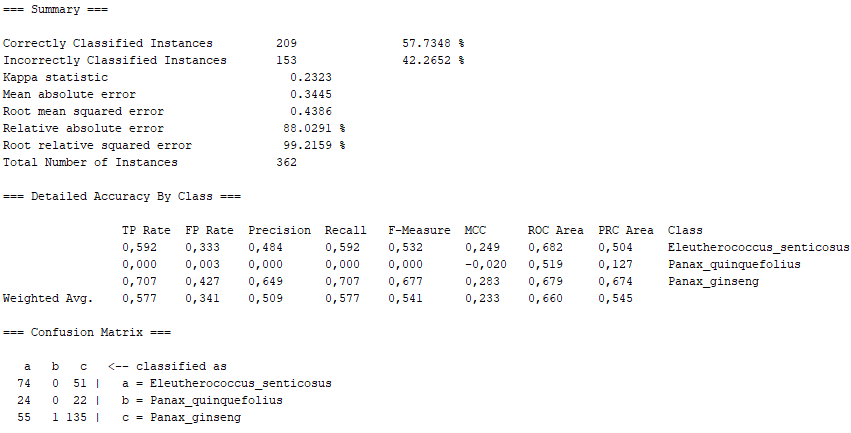
Having seen all the results obtained, we can conclude some aspects.
On the one hand, there are several algorithms that, although they present high percentages of "Correctly Classified Instances", do not comply with good values in the "True Positive Rate" or in the Confusion Matrix itself. Above all, these insufficient values correspond to the photographs representing the Panax quinquefolius plant, because this is the plant for which the fewest photographs have been submitted. The algorithms that represent this disadvantage are functions.SimpleLogistic, functions.DI4jMIpClassifier, trees.RandomForest, trees.RandomTree and bayes.BayesNet.
On the other hand, taking into account the error made by us in the imbalance between number of images, there are other algorithms that even present passable values. We would have lazy.KStar with more than 66% of "Correctly Classified Instances", maintaining a 0.5 in the "True Positive Rate" corresponding to the Panax Quinquefolius, as well as a sufficiently marked diagonal in the Confusion Matrix. Similarly, lazy.IBk has very similar values, as it is also of the "lazy" class. Furthermore, function.SMO also shows sufficient values, with the difference that they are not as marked as in the "lazy" class, especially as far as Panax Quinquefolius is concerned. Like this, fuctions.Logistic also lags behind the "lazy" algorithms, since it is of the "functions" class, which has proved not to be as effective in our problem with the Panax Quinquefolius. Finally, we have trees.J48 which, although it has better values than the "functions" class, is not superior to the "lazy" class, thus falling between the last two.
Thus, we can conclude that, taking into account our errors with the number of photographs and treating the programme in a general way, both lazy.KStar and lazy.IBk were the most efficient algorithms among the ten presented.